函数的奇偶性习题

前言

利用函数的奇偶性可以解决以下问题：求函数值，求解析式，求解析式中的参数的值，做函数图像，求特殊值。

奇偶函数

常见的奇函数，最好借助奇偶性和单调性能掌握其函数的图像；

$f(x)=kx$；

$f(x)=x^3$；

$f(x)=x^k$($k$为奇数)；

$y=Asin\omega x$；

$y=e^x-e^{-x}$；

$y=2^x-2^{-x}$；

$y=ln\frac{x+1}{x-1}$；

$f(x)=x+\frac{k}{x}(k\neq 0)$；

$g(x)=lg(\sqrt{sin^2x+1}+sinx)$；

$g(x)=x^3+lg(\sqrt{x^2+1}+x)$；

$f(x)=x^3\pm 3sinx$；

$f(x)=ln(\sqrt{x^2+1}\pm x)$；

$g(x)=\cfrac{2^x-1}{2^x+1}$；

$f(x)=\cfrac{2^x+1}{2^x-1}$；

$h(x)=\cfrac{a^x-1}{a^x+1}(a>0，a\neq 1)$；

$g(x)=x+\cfrac{1}{x}$；

$f(x)=x-\cfrac{1}{x}$；

$h(x)=x^3+\cfrac{1}{x^3}$；

$g(x)=x^3-\cfrac{1}{x^3}$；

$h(x)=\cfrac{2^x-2^{-x}}{2^x+2^{-x}}$；

$f(x)=log_2\cfrac{1-x}{1+x}$；

备注：需要特别注意这种运算技巧，\(g(-x)=\cfrac{2^{-x}-1}{2^{-x}+1}=\cfrac{(2^{-x}-1)\cdot 2^x}{(2^{-x}+1)\cdot 2^x}=\cfrac{1-2^{x}}{2^{x}+1}=-g(x)\)

常见的偶函数，最好借助奇偶性和单调性能掌握其函数的图像；

$f(x)=x^2$；

$y=k|x|(k\in R)$；

$y=e^{|x|}$；

$f(x)=x^k$($k$为偶数)；

$y=Acos \omega x+k$；

$y=e^x+e^{-x}$；

$y=2^x+2^{-x}$；

$f(x)=ln(1+|x|)$；

$f(x)=\frac{|x|}{x^2+1}$；

$h(x)=ln(2^x+2^{-x})$；

$f(x)=x^2+\cfrac{1}{x^2}$；

$f(x)=x^4+\cfrac{1}{x^4}$；

运算技巧

涉及偶函数的考查中，用到最多见的变形是使用\(f(x)=f(-x)=f(|x|)\)；为什么？^[1]

当函数中有对数符号时，判断奇偶性利用公式\(f(-x)+f(x)=0\)最方便。

如果函数\(f(x)\)为奇函数且有最值，则\(f(x)_{max}+f(x)_{min}=0\) ，具体详见下例所述：

设函数\(f(x)=3+x+\sqrt{1-x^{2}}\cdot\cfrac{2^{x}-1}{2^{x}+1}\)的最大值为\(M\)，最小值为\(N\)，则\(M+N\)的值是【】

$A.3$ $B.2$ $C.6$ $D.4$

详解： 令\(g(x)=x+\sqrt{1-x^{2}}\cdot\cfrac{2^{x}-1}{2^{x}+1}\)，

由\(1-x^{2}\geqslant 0\)得到定义域为\(-1\leqslant x\leqslant 1\)，

\(g(-x)=-x+\sqrt{1-(-x)^{2}}\cdot\cfrac{2^{-x}-1}{2^{-x}+1}\)

\(=-x+\sqrt{1-(-x)^{2}}\cdot\cfrac{(2^{-x}-1)\cdot 2^x}{(2^{-x}+1)\cdot 2^x}\)

\(=-x+\sqrt{1-x^{2}}\cdot\cfrac{1-2^{x}}{1+2^{x}}\)

\(=-x-\sqrt{1-x^{2}}\cdot\cfrac{2^{x}-1}{1+2^{x}}=-g(x)\)

则函数\(g(x)\)为定义域为\([-1,1]\)上的奇函数， \(g(x)_{\max}+g(x)_{\min}=0\)，

所以\(M+N=g(x)_{\max}+3+g(x)_{\min}+3=6\)，故选 \(C\)。

设函数\(f(x)=\cfrac{(x+1)^{2}+\sin x}{x^{2}+1}\)，若\(f(-a)=M\)，\(f(a)=m\)，则\(M+m\)=_____________.

分析： 根据分式函数的性质，进行转化，构造奇函数，利用奇函数的性质，即可求得答案.

由于\(f(x)=\cfrac{(x+1)^{2}+\sin x}{x^{2}+1}\)\(=\)\(\cfrac{x^{2}+2x+1+\sin x}{x^{2}+1}\)\(=\)\(1+\cfrac{\sin x+2x}{x^{2}+1}\)

则\(f(x)-1=\cfrac{\sin x+2 x}{x^{2}+1}\)，令\(g(x)=\cfrac{\sin x+2x}{x^{2}+1}\)

由于\(g(x)\)的定义域为\(R\)，\(g(-x)=\cfrac{-\sin x-2x}{x^{2}+1}=-g(x)\)，

故\(g(x)=\cfrac{\sin x+2x}{x^{2}+1}\)是定义域为\(R\)的奇函数，

则\(g(-a)+g(a)=0\)，又\(g(-a)=f(-a)-1=M-1\)，\(g(a)=f(a)-1=m-1\)，

所以\(M-1+m-1=0\)，则\(M+m=2\). 故答案为: \(2\).

典例剖析

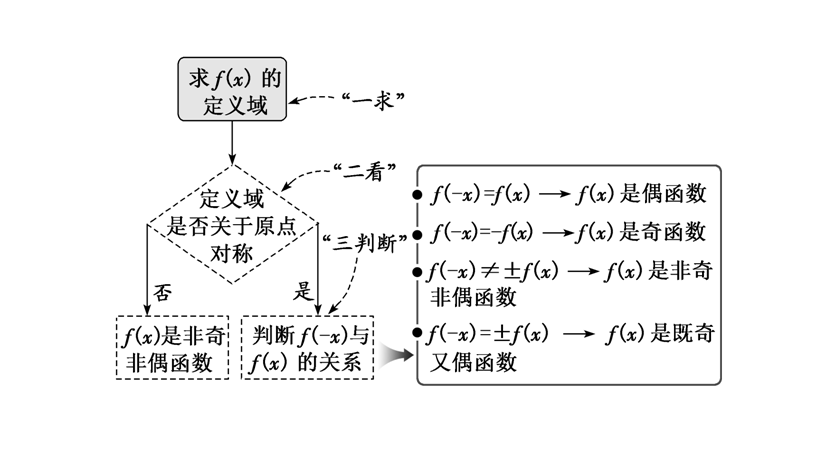
• 判断奇偶性；[注意对解析式的必要和有效化简]

判断函数\(f(x)=\cfrac{\sqrt{1-x^2}}{2-|x+2|}\)的奇偶性。

分析：研究函数的性质，一般先要求定义域，由题目可知\(\begin{cases}1-x^2\ge 0\\2-|x+2|\neq 0\end{cases}\)，

解得定义域是\([-1，0) \cup (0，1]\)，

这样函数就能简化为\(f(x)=\cfrac{\sqrt{1-x^2}}{2-|x+2|}=\cfrac{\sqrt{1-x^2}}{2-x-2}=\cfrac{\sqrt{1-x^2}}{-x}\)，

所以\(f(-x)=-f(x)\)，故函数是奇函数。

定义两种运算：\(a\otimes b=\sqrt{a^2-b^2}\)，\(a\oplus b=\sqrt{(a-b)^2}\)，则\(f(x)=\cfrac{2\otimes x}{2-(x\oplus 2)}\)的奇偶性如何？

分析：由定义的运算可知\(2\otimes x=\sqrt{2^2-x^2}=\sqrt{4-x^2}\)，\(x\oplus 2=\sqrt{(x-2)^2}=|x-2|\)，

于是\(f(x)=\cfrac{\sqrt{4-x^2}}{2-|x-2|}\)，仿例2先求得定义域为\([-2，0)\cup(0，2]\)，

故\(f(x)=\cfrac{\sqrt{4-x^2}}{2-(2-x)}=\cfrac{\sqrt{4-x^2}}{x}\)，满足\(f(-x)=-f(x)\)，故函数\(f(x)\)为奇函数。

反思：研究函数的性质，一般都要求定义域优先原则。

【复合函数的奇偶性判断】【河南省信阳市2019届高三第二次调研】已知函数\(f(x)=\left\{\begin{array}{l}{x^2+2x，x\geqslant 0}\\{x^2-2x，x<0}\end{array}\right.\)，则下列函数为奇函数的是【】

$A.f(sinx)$ $B.f(cosx)$ $C.x\cdot f(sinx)$ $D.x^2\cdot f(cosx)$

分析：先做出函数\(f(x)\)的图像，由图像可知\(f(x)\)为偶函数；

对于选项\(A\)，令\(F(x)=f(sinx)\)，则\(F(-x)=f(sin(-x))=f(-sinx)=f(sinx)=F(x)\)，故\(f(sinx)\)为偶函数；

对于选项\(B\)，令\(F(x)=f(cosx)\)，则\(F(-x)=f(cos(-x))=f(cosx)=F(x)\)，故\(f(cosx)\)为偶函数；

对于选项\(C\)，奇函数乘以偶函数为奇函数，故\(x\cdot f(sinx)\)为奇函数；

对于选项\(D\)，偶函数乘以偶函数为偶函数，故\(x^2\cdot f(cosx)\)为偶函数；

故选\(C\).

• 利用奇偶性求值；

【2020佛山一模】已知\(f(x)={2}^{x}+\cfrac{a}{2^{x}}\)为奇函数，\(g(x)=bx-\log_{2}(4^{x}+1)\)为偶函数，则\(f(ab)=\)【】

$A.\cfrac{17}{4}$ $B.\cfrac{5}{2}$ $C.-\cfrac{15}{4}$ $D.-\cfrac{3}{2}$

分析：由于函数\(f(x)\)为奇函数，且定义域为\(R\)，故其必满足\(f(0)=0\)，即\(2^0+\cfrac{a}{2^0}=0\)，解得\(a=-1\)；

又由于函数\(g(x)\)为偶函数，定义域为\(R\)，可以用两个思路[①特殊值法，②定义法]求解参数的值；

①特殊值法，由\(g(-1)=g(1)\)，即\(-b-\log_2(4^{-1}+1)=b-\log_2(4^1+1)\)，

即\(2b=\log_25-\log_2\cfrac{5}{4}\)，即\(2b=\log_25+\log_2\cfrac{4}{5}=\log_24=2\)，解得\(b=1\)；

②定义法，由\(g(-x)=g(x)\)恒成立，即\(-bx-\log_2(4^{-x}+1)=bx-\log_2(4^x+1)\)恒成立，

即\(2bx=\log_2(4^x+1)-\log_2(\cfrac{1+4^x}{4^x})\)，即\(2bx=\log_2(4^x+1)+\log_2(\cfrac{4^x}{1+4^x})=\log_24^x=2x\)，

即\(2bx-2x=0\)，即\(2x(b-1)=0\)对\(\forall x\in R\)恒成立，即\(b=1\)；

则\(f(ab)=f(-1)=2^{-1}-\cfrac{1}{2^{-1}}=-\cfrac{3}{2}\)，故选\(D\)；

[求函数中的参数值]【2017\(\cdot\)深圳模拟】若函数\(f(x)=\cfrac{x}{(2x+1)(x-a)}\)是奇函数，则实数 \(a\) 的值是【\(\quad\)】

$A.\cfrac{1}{2}$ $B.\cfrac{2}{3}$ $C.\cfrac{3}{4}$ $D.-\cfrac{1}{2}$

【法1】：由函数\(f(x)\)为奇函数，则满足\(f(-x)=-f(x)\)，

\(f(x)=\cfrac{x}{(2x+1)(x-a)}=\cfrac{x}{2x^2+(1-2a)x-a}\)，

\(f(-x)=\cfrac{-x}{(-2x+1)(-x-a)}=\cfrac{-x}{2x^2-(1-2a)x-a}\)，

则\(\cfrac{-x}{2x^2-(1-2a)x-a}=\cfrac{-x}{2x^2+(1-2a)x-a}\)应该恒成立，

只需要\(-(1-2a)=1-2a\)，解得\(a=\cfrac{1}{2}\)；故选\(A\)；

【法2】：由于定义域中有\(-1，1\)，故必然满足\(f(-1)=-f(1)\)，解得\(a=\cfrac{1}{2}\)；故选\(A\)；和法1相比，是特值验证。

【法3】：由于奇函数的定义域关于原点对称，令\(2x+1=0\)得到\(x=-\cfrac{1}{2}\)，故可知定义域中没有\(x=-\cfrac{1}{2}\)；

令\(x-a=0\)得到\(x=a\)，故定义域中必然没有\(x=a\)，故\(a=\cfrac{1}{2}\)；故选\(A\)；

【法4】：\(f(x)=\cfrac{x}{(2x+1)(x-a)}=\cfrac{x}{2x^2+(1-2a)x-a}\)，由于分子函数为奇函数，要是\(f(x)\)为奇函数，则分母函数\(y=2x^2+(1-2a)x-a\)为二次函数，

要是偶函数，则\(1-2a=0\)，解得\(a=\cfrac{1}{2}\)；故选\(A\)；

【2022年高考文科数学全国卷乙卷第16题】 若 \(f(x)=\ln|a+\dfrac{1}{1-x}|+b\) 是奇函数， 则 \(a=\) _______，\(b=\) _________.

解析：因为函数 \(f(x)=\ln|a+\dfrac{1}{1-x}|+b\) 为奇函数， 所以其定义域关于原点对称 .

由 \(a+\dfrac{1}{1-x}\neq 0\) ^[2] ，分式化为整式得到此处的分式化为整式的变形就显得非常关键，因为只有这样才能产生两个因式相乘不等于零的形式，才有可能满足定义域关于原点对称。对思维的考查凸显的非常明显，所以我感觉这个题目命制的相当成功。，\((1-x)(a+1-ax)\neq 0\)，

由上式中 \(1-x\neq 0\) 显然能得到 \(x\neq 1\)，

故由 \(a+1-ax\neq 0\) 应该得到 \(x\neq -1\) 才能满足其定义域关于原点对称，

由 \(a+1-ax=0\)能得到 \(x=\dfrac{a+1}{a}\)，令\(x=-1\)，即\(\dfrac{a+1}{a}=-1\) ，解得: \(a=-\dfrac{1}{2}\)，

此时函数的定义域为 \((-\infty,-1)\cup(-1,1)\cup(1,+\infty)\)， 再由 \(f(0)=0\) 可得 \(b=\ln 2\).

即 \(f(x)=\ln|-\dfrac{1}{2}+\dfrac{1}{1-x}|+\ln 2=\ln|\dfrac{1+x}{1-x}|\)，在定义域内满足 \(f(-x)=-f(x)\)， 符合题意 .

故 \(a=-\dfrac{1}{2}\)， \(b=\ln 2\).

【求区间的参数值】设函数\(f(x)\)是定义在区间\([-2b，3+b]\)上的偶函数，即告诉了\(b\)的值；

分析：由于函数具有奇偶性，故定义域关于原点对称，即\(-2b+3+b=0\)，解得\(b=3\)；

【2019届高三理科函数的奇偶性周期性课时作业第5题】设函数\(f(x)=\left\{\begin{array}{l}{log_2(1-x)，x<0}\\{g(x)+1，x>0}\end{array}\right.\)，若\(f(x)\)为奇函数，求\(g(3)\)值。

法1：利用奇偶性，求得\(g(x)\)的解析式，再求\(g(3)\)，略。

法2：【整体有奇偶性，但部分没有奇偶性】\(f(3)=g(3)+1\)，则\(g(3)=f(3)-1\)，由于\(f(x)\)为奇函数，则\(f(3)=-f(-3)\)，

故\(g(3)=f(3)-1=-f(-3)-1=-log_2(1+3)-1=-3\)，故\(g(3)=-3\)。

已知函数\(f(x)=\cfrac{x^2+x+1}{x^2+1}\)，若\(f(a)=\cfrac{2}{3}\)，求\(f(-a)\)的值；

分析：在使用函数的奇偶性解题是要注意函数“整体有奇偶性”和“局部有奇偶性”，

\(f(x)=\cfrac{x^2+1+x}{x^2+1}=1+\cfrac{x}{x^2+1}\)，而原函数的局部\(g(x)=\cfrac{x}{x^2+1}\)有奇偶性，

是奇函数，故\(f(-x)+f(x)=1+g(-x)+1+g(x)=2\)，故\(f(-a)+f(a)=2\)，

解得\(f(-a)=2-\cfrac{2}{3}=\cfrac{4}{3}\).

其实，本题还能推出函数\(f(x)\)关于点\((0，1)\)对称。

反思：注意函数“整体有奇偶性”和“局部有奇偶性”，恰当利用，能方便我们的解题。

【信息题】设函数\(f(x)=(a^2-4)x^5+2x^3+(a-2)x+sin2x+1\)，若\(f(3)=10\)，则\(f(-3)\)=【】

$A.-8$ $B.-10$ $C.-9$ $D.-11$

分析：令\(g(x)=(a^2-4)x^5+2x^3+(a-2)x+sin2x\)，则\(g(x)\)为奇函数，则\(g(-x)=-g(x)\)，

这样\(f(x)=g(x)+1\)，由于\(f(3)=g(3)+1=10\)，

令\(f(-3)=m=g(-3)+1\)，两式相加得到，

\(g(3)+1+g(-3)+1=10+m\)，即\(g(3)+g(-3)+2=10+m\)，即\(2=10+m\)，

解得\(m=-8\)，即\(f(-3)=-8\)，故选\(A\)。

• 利用奇偶性求取值范围[解不等式]；

【2016.天津高考】已知\(f(x)\)是定义在\(R\)上的偶函数，且在区间\((-\infty，0)\)上单调递增。若实数\(a\)满足\(f(2^{|a-1|})>f(-\sqrt{2})\)，则\(a\)的取值范围是【】

$A.(-\infty，\cfrac{1}{2})$ $B.(-\infty，\cfrac{1}{2})\cup (\cfrac{3}{2}，+\infty)$ $C.(\cfrac{1}{2}，\cfrac{3}{2})$ $D.(\cfrac{3}{2}，+\infty)$

分析：由偶函数可知，\(f(x)\)总满足\(f(x)=f(-x)=f(|x|)\)，\(f(x)\)在区间\((0，+\infty)\)上单调递减，

故将已知条件转化为\(f(2^{|a-1|})>f(|-\sqrt{2}|)=f(\sqrt{2})\)，

利用在区间\((0，+\infty)\)上单调递减得到\(2^{|a-1|}<2^{\frac{1}{2}}\)，则有\(|a-1|<\cfrac{1}{2}\)，

解得\(a\in (\cfrac{1}{2}，\cfrac{3}{2})\)。

【2019宝鸡中学试题】定义在\(R\)上的偶函数\(f(x)\)满足：对任意的\(x_1\)，\(x_2\in(-\infty，0](x_1\neq x_2)\)，有\((x_1-x_2)[f(x_2)-f(x_1)]<0\)，且\(f(2)=0\)，则不等式\(\cfrac{3f(x)+f(-x)}{5x}<0\)的解集为_____________。

分析：对任意的\(x_1\)，\(x_2\in(-\infty，0](x_1\neq x_2)\)，有\((x_1-x_2)[f(x_2)-f(x_1)]<0\)，

即\(x_1\)，\(x_2\in(-\infty，0](x_1\neq x_2)\)，有\((x_1-x_2)[f(x_1)-f(x_2)]>0\)，

即函数在\((-\infty，0]\)上单调递增，故由偶函数可知，函数在\([0，+\infty)\)上单调递减，

又由于偶函数，则\(f(2)=f(-2)=0\)，做出适合题意的示意图如下，

且不等式\(\cfrac{3f(x)+f(-x)}{5x}<0\)可以转化为\(\cfrac{3f(x)+f(x)}{5x}<0\)

即\(\cfrac{f(x)}{x}<0\)，由图可知，解为\(-2<x\leqslant 0\)或\(x>2\)。

故解集为\((-2，0]\cup (2，+\infty)\)。

设偶函数\(f(x)\)满足\(f(x)=2^x-4(x≥0)\)，则不等式的解集\(\{x\mid f(x-2)>0\}\)是【】

$A.\{x \mid x<-2 或 x>4\}$ $B.\{x \mid x<0 或 x>4\}$ $C.\{x\mid x<0 或 x>6\}$ $D.\{x\mid x<-2 或 x>2\}$

分析：先利用奇偶性求得函数的解析式\(f(x)=\begin{cases}2^x-4&x\ge0\\2^{-x}-4&x<0\end{cases}\)，如何求，接下来

[法1]：图像法，作出函数\(f(x)\)的图像，变换得到\(f(x-2)\)的图像，

从而利用图像解得不等式\(f(x-2)>0\)。图像

[法2]：代数法，由\(f(x)\)的解析式得到函数\(f(x-2)\)的解析式

\(f(x-2)=\begin{cases}2^{x-2}-4&x-2\ge0\\2^{-(x-2)}-4&x-2<0\end{cases}\)，

即\(f(x-2)=\begin{cases}2^{x-2}-4&x\ge2\\2^{2-x}-4&x<2\end{cases}\)，

故\(f(x-2)>0\)可等价转化为\(\begin{cases}x\ge 2\\2^{x-2}-4>0\end{cases}\)

或者\(\begin{cases}x<2\\2^{2-x}-4>0\end{cases}\)，

解得\(x<0\)或\(x>4\)，故选\(B\).

[法3]：利用偶函数的性质，\(f(-x)=f(x)=f(|x|)\)，

由\(f(x)=2^x-4(x\ge 0)\)，可知偶函数\(f(x)\)在\([0 ，+\infty)\)上单调递增，且有\(f(2)=0\)，

故所求不等式\(f(x-2)>0\)，可以转化为\(f(x-2)>f(2)\)，

由偶函数再次转化为\(f(|x-2|)>f(|2|)\)，由\(f(x)\)在\([0 ，+\infty)\)上单调递增，

可知\(|x-2|>2\)，解得\(x<0\)或\(x>4\)，故选\(B\).

函数\(f(x)\)在\([0，+\infty)\)上是增函数，\(g(x)=-f(|x|)\)，若\(g(lgx)>g(1)\)，求\(x\)的范围。

分析：由于\(f(x)\)在\([0，+\infty)\)上是增函数，故\(y=-f(x)\)在\([0，+\infty)\)上是减函数，

又函数\(g(x)=-f(|x|)\)是偶函数，故在\([0，+\infty)\)上是减函数，\((-\infty，0]\)上是增函数，

由函数\(g(x)\)是偶函数，则\(g(lgx)>g(1)\)等价转化为\(g(|lgx|)>g(1)\)，

又由于在\([0，+\infty)\)上是减函数，故有\(|lgx|<1\)

即\(-1<lgx<1\)，解得\(\cfrac{1}{10}<x<1\)。

【2018·珠海月考】已知定义在\(R\)上的奇函数\(y＝f(x)\)在\((0，＋\infty)\)上单调递增，且\(f(\cfrac{1}{2})=0\)，则满足\(f(log{\frac{1}{9}}x)>0\) 的$ x$ 的集合为_________。

分析：由于\(y＝f(x)\)在\((0，＋\infty)\)上单调递增，且为奇函数，

则可知函数在\((-\infty，0)\)上单调递增，又\(f(\cfrac{1}{2})=0\)，

则可知\(f(-\cfrac{1}{2})=0\)，又由于函数定义在\(R\)上，则\(f(0)=0\)，

做出大致示意图如下，

由图像可得，

故有\(log{\frac{1}{9}}x>\cfrac{1}{2}\)或\(-\cfrac{1}{2}<log{\frac{1}{9}}x<0\)

即\(log{\frac{1}{9}}x>\cfrac{1}{2}=log{\frac{1}{9}}(\cfrac{1}{9})^{{\frac{1}{2}}}=log{\frac{1}{9}}{\cfrac{1}{3}}\)

或\(log{\frac{1}{9}}3<log{\frac{1}{9}}x<log{\frac{1}{9}}1\)

解得\(0<x<\cfrac{1}{3}\)或\(1<x<3\)，

故所求集合为\(\{x\mid 0<x<\cfrac{1}{3}或1<x<3 \}\)。

【2019届高三理科函数的奇偶性周期性课时作业第6题】设函数\(f(x)=ln(\cfrac{2}{1-x}+a)\)是奇函数，则使\(f(x)<0\)的\(x\)的取值范围是__________。

分析：先求定义域，令\(\cfrac{2}{1-x}+a>0\)，即\(\cfrac{a(x-1)+2}{x-1}>0\)，

由于函数的定义域对称，则方程\([a(x-1)+2](x-1)=0\)的两个根之和为零，

即\(\cfrac{2}{a}+1+1=0\)，解得\(a=-1\)，代入\(\cfrac{2}{1-x}+a>0\)，

即\(\cfrac{2}{1-x}-1>0\)，解得定义域为\((-1，1)\)，

又\(f(x)<0=f(0)\)，又函数\(f(x)\)在区间\([0，1)\)上单调递增，

故\(x<0\)，又\(-1<x<1\)，则\(x\in (-1，0)\)。

【2019届高三理科数学二轮资料用题】已知定义在\(R\)上的奇函数\(f(x)\)单调递增，且\(g(x)=|f(x)|\)，则不等式\(g(x)-g(2x-6)<0\)的解集是【】

$A(2，6)$ $B(-6，-2)$ $C(-\infty，2)\cup(6，+\infty)$ $D(-\infty，-6)\cup(-2，+\infty)$

分析：\(g(x)\)为偶函数，且在\([0，+\infty)\)上单调递增，\(g(|x|)<g(|2x-6|)\)，故\(|x|<|2x-6|\)，解得 \(x\in (-\infty，2)\cup(6，+\infty)\)，故选\(C\).

【2018山东威海二模】已知函数\(f(x)=xcosx-sinx-\cfrac{1}{3}x^3\)，则不等式\(f(2x+3)+f(1)<0\)的解集为【】

$A(-2，+\infty)$ $B(-\infty，-2)$ $C(-1，+\infty)$ $D(-\infty，-1)$

分析：由于\(f(-x)=-f(x)\)，古函数\(f(x)\)为奇函数，又由于\(f'(x)=cosx+x(-sinx)-cosx-x^2\)，

则\(f'(x)=-x(sinx+x)\leq 0\)，(此处针对\(x\)分类讨论即可判断正负)

故函数\(f(x)\)在\(R\)上单调递减，又由于\(f(2x+3)<-f(1)=f(-1)\)，故\(2x+3>-1\)，解得\(x>-2\)，故选\(A\).

【2019届高三理科数学第三轮模拟训练题】已知函数\(f(x)=e^{-x}-x^3-e^x\)，则不等式\(|f(4x-7)|<f(-1)\)的解集为【】

$A(-1，1)$ $B(\cfrac{3}{2}，2)$ $C(-\infty，\cfrac{3}{2})\cup(2，+\infty)$ $D(-\infty，-1)\cup(1，+\infty)$

分析：由于\(f(x)=e^{-x}-e^x-x^3\)为奇函数，且\(-f(-1)=f(1)\)，\(f(0)=0\)，在\(R\)上单调递减，

故 \(|f(4x-7)|<f(-1)\) 等价于 \(-f(-1)<f(4x-7)<f(-1)\)，即 \(f(1)<f(4x-7)<f(-1)\)，

则利用单调性去掉对应法则符号，得到 \(-1<4x-7<1\) ，解得 \(\cfrac{3}{2}<x<2\) ，故选 \(B\)。

【2019届高三理科数学三轮模拟试题】已知函数\(f(x)\)为偶函数，且当\(x>0\)时，\(f'(x)<0\)，则\(f(2x)>f(x+3)\)的解集是【】

$A.(-\infty，-1)$ $B.(-1，+\infty)$ $C.(3，+\infty)$ $D.(-1，3)$

分析：由\(x>0\)时，\(f'(x)<0\)，可知函数\(f(x)\)在区间\((0，+\infty)\)上单调递减，

又由于函数\(f(x)\)为偶函数，由\(f(2x)>f(x+3)\)可得，\(f(|2x|)>f(|x+3|)\)，

则有\(|2x|<|x+3|\)，解得\(-1<x<3\)，故选\(D\)。

• 利用奇偶性证明；

【需要构造函数】若\(\alpha，\beta\in [-\cfrac{\pi}{2}，\cfrac{\pi}{2}]\)，且\(\alpha\cdot sin\alpha-\beta\cdot sin\beta>0\)，则下列结论正确的是【】

$A.\alpha > \beta$ $B.\alpha+\beta > 0$ $C.\alpha < \beta$ $D.\alpha^2 > \beta^2$

分析：由\(\alpha\cdot sin\alpha-\beta\cdot sin\beta>0\)，得到\(\alpha\cdot sin\alpha>\beta\cdot sin\beta\)，左右两边的结构一模一样，故联想到构造函数

令\(g(x)=x\cdot sinx\)，则上述条件可表述为\(g(\alpha)>g(\beta)\)，要去掉符号\(g\)，我们就得研究函数的性质，尤其是奇偶性和单调性。

由于函数\(g(-x)=(-x)\cdot sin(-x)=x\cdot sinx=g(x)\)，故函数\(g(x)\)为偶函数；

当\(x\in[0，\cfrac{\pi}{2}]\)，\(g(x)=x\cdot sinx\)单调递增，^[3]

利用偶函数的性质，将\(g(\alpha)>g(\beta)\)等价转化为\(g(|\alpha|)>g(|\beta|)\)，

故\(|\alpha|>|\beta|\)，则有\(\alpha^2>\beta^2\)，选\(D\)。

【2018合肥质检】已知函数\(f(x)=sin^4x+cos^4x\)，\(x\in [-\cfrac{\pi}{4}，\cfrac{\pi}{4}]\)，若\(f(x_1)<f(x_2)\)，则一定有【】

$A.x_1 < x_2$ $B.x_1 > x_2$ $C.x_1^2 < x_2^2$ $D.x_1^2 > x_2^2$

分析：\(f(x)=(sin^2x+cos^2x)^2-2sin^2xcos^2x=1-\cfrac{1}{2}\cdot 2^2\sin^2xcos^2x=1-\cfrac{1}{2}(sin2x)^2\)

\(=1-\cfrac{1}{2}\cdot\cfrac{1-cos4x}{2}=\cfrac{1}{4}cos4x+\cfrac{3}{4}\)，

则函数\(f(x)\)为偶函数，由\(f(x_1)<f(x_2)\)，则必有\(f(|x_1|)<f(|x_2|)\)

且在区间\([0，\cfrac{\pi}{4}]\)上单调递减，则有\(|x_1|>|x_2|\)，故\(x_1^2>x_2^2\)，故选\(D\)。

【2018·太原模拟】已知函数\(f(x)=x(e^x-\cfrac{1}{e^x})\)，若\(f(x_1)<f(x_2)\)，则【】

$A.x_1 > x_2$ $B.x_1+x_2=0$ $C.x_1 < x_2$ $D.x_1^2 < x_2^2$

分析：先研究清楚函数的组成部分的性质，

\(y=x\)奇函数，在\(R\)上单调递增；\(y=e^x-e^{-x}\)奇函数，在\(R\)上单调递增(增+增)；

故\(f(x)=x(e^x-\cfrac{1}{e^x})\)为偶函数，在\([0，+\infty)\)上单调递增，在\((-\infty，0]\)上单调递减。

故由偶函数的性质，\(f(x_1)<f(x_2)\)，

等价于\(f(|x_1|)<f(|x_2|)\)，又函数在\([0，+\infty)\)上单调递增，

即有\(|x_1|<|x_2|\)，即 \(x_1^2<x_2^2\)，故选\(D\)。

【2018河南南阳期末】设\(f(x)=e^{1+sinx}+e^{1-sinx}\)，\(x_1，x_2\in[-\cfrac{\pi}{2}，\cfrac{\pi}{2}]\)，且\(f(x_1)>f(x_2)\)，则下列结论必然成立的是【】

$A.x_1 > x_2$ $B.x_1+x_2 > 0$ $C.x_1 < x_2$ $D.x_1^2 > x_2^2$

分析：\(f(-x)=e^{1-sinx}+e^{1+sinx}=f(x)\)，故函数\(f(x)\)为偶函数，

又当\(x\in[0，\cfrac{\pi}{2}]\)，\(f'(x)=e^{1+sinx}\cdot cosx+e^{1-sinx}\cdot (-cosx)=cosx(e^{1+sinx}-e^{1-sinx})>0\)，

故函数\(f(x)\)在\([0，\cfrac{\pi}{2}]\)上单调递增，则由\(f(x_1)>f(x_2)\)得到，

\(f(|x_1|)>f(|x_2|)\)，则有\(|x_1|>|x_2|\)，则\(x_1^2>x_2^2\)，故选\(D\).

设函数\(f(x)=x^3+lg(\sqrt{x^2+1}+x)\)，则对任意实数\(a\)，\(b\)，若\(a+b\ge 0\)，则有【】

$A.f(a)+f(b)\leq 0$ $B.f(a)+f(b)\ge 0$ $C.f(a)-f(b)\leq 0$ $D.f(a)+f(b)\ge 0$

分析：函数\(f(x)\)满足条件，\(f(-x)+f(x)=0\)，故为奇函数，又函数在\(R\)上单调递增，故由\(a\ge -b\)，得到\(f(a)\ge f(-b)\)，即\(f(a)\ge -f(b)\)，则\(f(a)+f(b)\ge 0\)，故选\(B\)。

不等式 \((x-1)^{\frac{2}{3}}>(3x+1)^{\frac{2}{3}}\) 的解集为 【\(\qquad\)】

$A.(-1,0)$ $B.(-\cfrac{1}{3},1)$ $C.(0,1)$ $D.(-\infty,0)\cup(1,+\infty)$

解析： 函数 \(y=f(x)=x^{\frac{2}{3}}\)，偶函数 ，故原不等式等价于 \(f(|x-1|)>f(|3x+1|)\)，

又函数 \(y=f(x)=x^{\frac{2}{3}}\)在 \([0,+\infty)\)上单调递增，故有 \(|x-1|>|3x+1|\)，

两边平方得到， \(|x-1|^2>|3x+1|^2\)，解得，\(x\in (-1,0)\)，故选 \(A\) .

---

1. 比如，已知定义在 \(R\) 上的函数 \(y=f(x)\) 满足 \(f(-x)-f(x)=0\)，且对在任意不相等的 \(x_1,x_2\in (-\infty,0]\) 有 \(\cfrac{x_1-x_2}{f(x_1)-f(x_2)}<0\) 成立，求解不等式\(f(x)>f(2-x)\)中\(x\)的取值范围。
   法1：[分类讨论，很繁琐的思路]
   先判断函数的定义域为\(R\)，且为偶函数；则可知在\((-\infty，0]\)上单调递减，在\([0，+\infty)\)上单调递增。
   若针对两个自变量\(x\)和\(2-x\)分类讨论，则得到以下四种情形：
   \(Ⅰ.\left\{\begin{array}{l}{x>0}\\{2-x\ge 0}\\{x>2-x}\end{array}\right.\)或者\(Ⅱ.\left\{\begin{array}{l}{x<0}\\{2-x\leq 0}\\{x<2-x}\end{array}\right.\)或者\(Ⅲ.\left\{\begin{array}{l}{x>0}\\{2-x\leq 0}\\{-x<2-x}\end{array}\right.\)或者\(Ⅳ.\left\{\begin{array}{l}{x<0}\\{2-x\ge 0}\\{-x>2-x}\end{array}\right.\)
   解Ⅰ得到，\(1<x\leq 2\)；解Ⅱ得到，\(x\in \varnothing\)；
   解Ⅲ得到，\(x\ge 2\)；解Ⅳ得到，\(x\in \varnothing\)；
   求并集得到\(x\)的取值范围为\(x>1\)，即\(x\in (1，+\infty)\)。
   法2：[利用偶函数的性质，简洁明快]先判断函数的定义域为\(R\)，在\((-\infty，0]\)上单调递减，在\([0，+\infty)\)上单调递增，且为偶函数；
   故由\(f(x)>f(2-x)\)变形得到，\(f(|x|)>f(|2-x|)\)，这样做的用意是将两个自变量整体强行放置到函数的单调递增区间上，便于利用单调性求解；
   故得到\(|x|>|2-x|\)，则\(x^2>(2-x)^2\)，解得\(x>1\)。即\(x\in (1，+\infty)\)。 ↩︎

2. 此处一般的思维都是由 \(a+\dfrac{1}{1-x}\neq 0\) 求解得到 \(x\neq 1+\dfrac{1}{a}\)，此时要么没法继续思考，要么艰难晦涩的这样思考，从形式上可以看到 \(x\neq1\)，故由定义域关于原点对称，还应该有 \(x\neq-1\)，现在 \(x\neq 1+\dfrac{1}{a}\)，故 应该有 \(1+\dfrac{1}{a}=-1\)，从而求解得到 \(a=-\dfrac{1}{2}\) . ↩︎

3. 原因一：\(x\in[0，\cfrac{\pi}{2}]\)时，\(y=x>0\)且单调递增，\(y=sinx>0\)且单调递增，故\(g(x)\)在\(x\in[0，\cfrac{\pi}{2}]\)上单调递增；
   原因二：导数法，\(g'(x)=sinx+x\cdot cosx\)，当\(x\in[0，\cfrac{\pi}{2}]\)时，\(g'(x)>0\)，故\(g(x)\)在\(x\in[0，\cfrac{\pi}{2}]\)上单调递增；
   综上，函数\(g(x)\)在\([-\cfrac{\pi}{2}，0]\)上单调递减，在\(x\in[0，\cfrac{\pi}{2}]\)上单调递增。 ↩︎